Казанский государственный технологический университет
(КГТУ)

420015, г. Казань, ул. К. Маркса д. 68
кафедра Автоматизации и информационных технологий
Кирпичников Александр Петрович,
Гайнуллин Рустем Нусратуллович
Герасимов Александр Викторович
Тел.: (8432) 194-272
Факс: (8432) 36-75-42
E-mail: kirpichnikov@kstu.ru ; gainullin@kstu.ru; gerasimov@kstu.ru

Комплексный метод определения электромагнитных и тепловых параметров высокочастотного индукционного разряда

Для адекватного управления плазменными процессами, позволяющими получать материалы и покрытия с уникальными физико-химическими свойствами, а также для разработки и оптимизации высокочастотных индукционных (ВЧИ) плазменных реакторов необходимо располагать информацией об основных электромагнитных и тепловых параметрах в зоне разряда.

Предложен комплексный метод решения  задачи восстановления полной картины распределения электромагнитного поля высокочастотного индукционного разряда (включая значение электропроводности плазмообразующего газа) по измеренным значениям амплитуды продольной составляющей магнитного поля в разряде.

В системе уравнений Максвелла, описывающей электромагнитное поле высокочастотного индукционного разряда, число величин характеризующих поле на единицу больше числа самих уравнений, то есть система уравнений незамкнута. Поэтому, считая заданной одну из величин, характеризующих поле, можно получить на выходе этой системы набор различных зависимостей, состоящих из электромагнитных величин и проводимости в разряде s.

В качестве входного параметра для решения системы уравнений Максвелла в данном случае используются данные магнитных измерений. Изменение величины магнитного поля по сечению разряда определяется поглощением электромагнитной энергии в проводящем слое газа. Поэтому при прочих равных условиях именно электропроводность газа определяет скорость изменения величины магнитного поля по радиусу разряда. Ввиду такой однозначной зависимости и становится возможным не прибегать к дополнительным уравнениям и решать задачу, оставаясь в рамках системы уравнений Максвелла.

Тем самым, используя взятое из эксперимента двухмерное числовое поле амплитуды H_z, можно попытаться путём совместного аналитического и численного решения системы максвелловских уравнений решить задачу восстановления полной пространственной структуры квазистационарного электромагнитного поля и проводимости в разряде s.

Основная проблема, с которой приходится сталкиваться в этой постановке задачи, заключается в следующем.

Исходя из максвелловских уравнений, проводимость может быть рассчитана по формуле:

  ,                        (1)

где H_z – амплитуда продольной компоненты магнитного поля в разряде,  - амплитуда азимутальной компоненты его электрического поля,  - фазовые углы этих же компонент соответственно и  c – скорость света в пустоте (в гауссовой системе единиц).

Если при решении уравнения (1) аппроксимировать амплитуду продольного магнитного поля в разряде H_z сглаженным кубическим сплайном, то проводимость обнаруживает резкую расходимость вблизи оси плазмоида, начиная с расстояний порядка одной трети радиуса плазменного сгустка. Очевидно, что это явление представляет собой прямое следствие неверной интерполяции H_z(r), вблизи нуля, и значит в данном случае  для решения задачи восстановления амплитуды H_z, как непрерывной функции радиальной координаты r, по конечному числу её экспериментально измеренных значений кубическими сплайнами пользоваться уже нельзя.

В настоящей работе, в результате проведённых исследований, предложен новый метод приближённого интегрирования системы  уравнений Максвелла для электромагнитного поля ВЧИ разряда, позволяющий однозначно и  точно  описать структуру решений этих уравнений вблизи оси плазмоида при малых значениях радиальной координаты r.

При этом приосевая часть двухмерной сплайн-поверхности, интерполирующей амплитуду продольного магнитного поля H_z(r, z) заменяется более точной зависимостью

                  ,                               

в которой постоянная

                                            ,                                                       

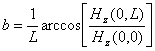где L —  длина плазмоида.

Эксперименты по измерению магнитного поля проводились на экспериментальном стенде, выполненном на базе высокочастотного плазмотрона ВЧИ 11-60/1,76 мощностью 60 кВт. Для работы в условиях термического разряда использовался специальный водоохлаждаемый магнитный зонд, допускающий длительную эксплуатацию при высоких температурах, свойственных такому типу разряда.

В результате магнитных измерений в разрядах на воздухе были получены радиальные распределения продольной составляющей магнитного поля H_z в различных сечениях по z, начиная от центрального сечения плазмоида,  вниз по потоку.

После обработки экспериментальной информации с помощью двумерной модели найдены радиальные профили основных электромагнитных величин, характеризующих ВЧИ разряд. Одновременно в каждой точке интегрирования в рамках модели ЛТР рассчитывались значения равновесной температуры T(s) и удельной мощности тепловыделения.

Полученная картина распределения тепловых полей и найденные при этом  зоны максимального выделения электромагнитной энергии играют основную роль в проблеме оптимизации высокотемпературных и плазменных устройствах, использующих принцип высокочастотного индукционного нагрева.

На основании проведенных авторами комплексных исследований ВЧИ разряда, основанных на предлагаемой методике, обнаружено явление коаксиальности высокочастотного индукционного разряда, заключающееся в том, что внутри плазмоида в каждом его поперечном сечении максимум проводимости, как функция радиуса, находится ближе к оси разряда, чем максимум плотности вихревого тока, а максимум плотности вихревого тока, в свою очередь, располагается ближе к оси, чем максимум полной вкладываемой в разряд мощности на единицу объёма, а также показано, что это явление является частью более общей зависимости, присущей высокочастотному индукционному разряду в целом.

Предлагаемый комплексный метод диагностики ВЧ низкотемпературной плазмы позволяет получить наиболее полную информацию о двумерном распределении основных электромагнитных и тепловых характеристик ВЧИ разряда. Он также может использоваться как независимый диагностический метод определения температуры в разряде, рассчитанной по обратной зависимости T = T(s) , особенно в тех случаях, когда применение оптических методов измерения по каким-либо причинам невозможно.

Важнейшие результаты: Разработан новый  комплексный  метод диагностики низкотемпературной плазмы высокочастотного индукционного разряда, позволяющий восстановить основные электромагнитные, электрофизические и тепловые параметры ВЧИ разряда конечной длины  по измеренным значениям амплитуды продольной компоненты магнитного поля в разряде.

Исследования по изучению электрофизических, теплообменных и газодинамических процессов в плазме высокочастотного индукционного (ВЧИ) и дугового разряда постоянного тока при атмосферном давлении.

Среди новых результатов наиболее значительными представляются следующие:

·    На основе анализа системы уравнений баланса энергии в приосевой области индуктора ВЧ-плазмотрона в рамках двухтемпературной модели получены уточнённые аналитические зависимости для расчета полей электронной температуры и атомно-ионной температуры тяжелых частиц в этой области в двухмерной постановке задачи; Проведено сравнение полученных профилей температуры электронного и атом-ионного газов с профилем температуры, рассчитанным по формуле одномерной однотемпературной модели Эккерта. Полученные результаты, расчетов, показывают, что разрыв между электронной и атомно-ионной температурами, который существует в приосевой области плазмоида, с большой точностью сохраняется вплоть до области, вплотную прилегающей к скин-слою (в данном случае скин-слой находится на расстоянии порядка 2 см от оси индуктора). Расчеты, проведенные для атомно-ионного газа, дают значения распределения температуры в приосевой области, имеющие характер “плато”, что хорошо согласуется с многочисленными как экспериментальными, так и расчетными данными. Для электронной температуры явление “плато” выражено слабее, хотя тоже имеет место. Показано, что расчеты, проведенные по формуле Эккерта тяготеют более к атомно-ионной температуре газа тяжелых частиц, чем к соответствующей электронной температуре.

·    Предложен метод расчета газовой и электронной температур в зоне теплоотвода дугового плазмотрона в рамках квазиравновесной двухтемпературной каналовой модели дугового разряда. Данный метод дает возможность при заданных параметрах разряда (сила тока в разряде, вкладываемая в разряд мощность и т. д.) получать распределение газовой и электронной температур в зависимости от радиальной координаты в непроводящей области дуги постоянного тока.

·    Предложен относительно простой алгоритм для оценки тепловых потоков, средней температуры и температурного профиля в канале электродугового плазмотрона, а также формы положительного столба в зависимости от величины расхода продуваемого через плазмотрон плазмообразующего газа. Получены расчетные профили температур, полученные по предлагаемым формулам для характерных значений температур стенки, вдува и канала для различных значений числа Пекле. Показано, что кривые, описывающие температурные поля в непроводящей зоне дугового разряда, при уменьшении скорости обдува стремятся к решению Штеенбека, которое является асимптотическим пределом для семейства кривых, описываемых полученными формулами.

Важнейшие результаты: В рамках двухтемпературной модели получены уточненные аналитические зависимости для расчета полей электронной и газовой температуры в приосевой области ВЧИ-разряда; предложена квазиравновесная двухтемпературная каналовая модель дуги постоянного тока, учитывающая отрыв атомно-ионной и электронной температур в непроводящей области дугового разряда; предложено описание парадокса  Энгеля-Штеенбека для дугового разряда.

Литература

1. Герасимов А.В., Кирпичников А.П. О балансе энергии плазмы высокочастотного индукционного разряда атмосферного давления вблизи оси плазменного сгустка // Прикладная физика. 2005. Т. 41. № 1. С. 57. 

2. Gerasimov A. V., Kirpichnikov A. P. Quasi-equilibrium channel model of an arc of a constant current  // Thermal Science 2003. №1. P. 101.

3. Герасимов А.В., Кирпичников А.П., Рачевский Л. А. Каналовая модель продольно обдуваемой дуги постоянного тока // Известия Вузов. Проблемы энергетики. 2004. №9-10. С. 36.